稳定可靠防死机的低功耗小体积显示主板I3399适用于工控医疗健康(4G&16G含屏幕)
应用领域: 工业电子
倾斜感测
*单轴倾斜感应
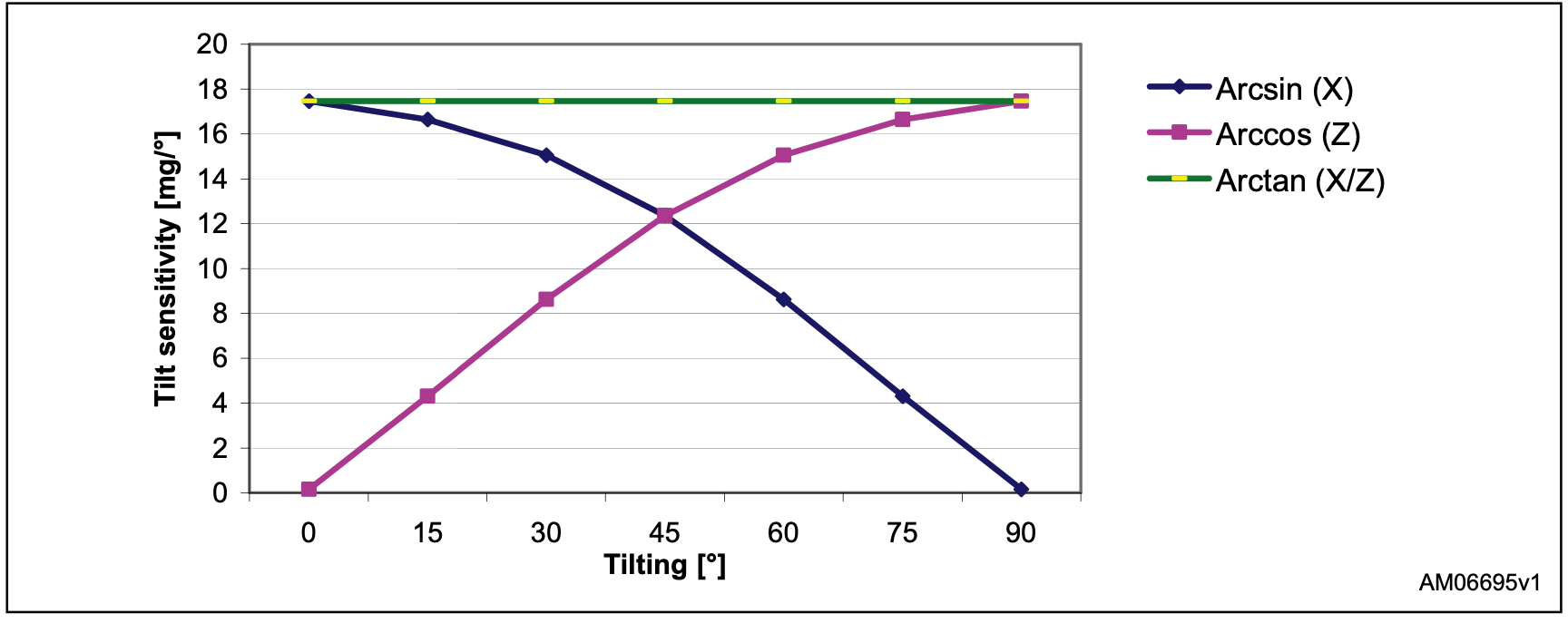
从图一和二中可以看出,当传感轴垂直于重力时,传感器对倾斜角度的变化最敏感。 在这种情况下,灵敏度约为17.45 mg /°[= sin(1°)-sin(0°)]。
由于正弦函数的微分函数,当传感轴接近+1 g或-1 g位置时,传感器具有较低的灵敏度(对倾斜角度变化的响应较小)。 在这种情况下,灵敏度仅为0.15 mg /°[= sin(90°)-sin(89°)]。 图三显示了不同倾斜角度下的灵敏度。 换句话说,正弦函数在[0°45°],[135°225°]和[315°360°]处具有良好的线性,如图二所示。
图一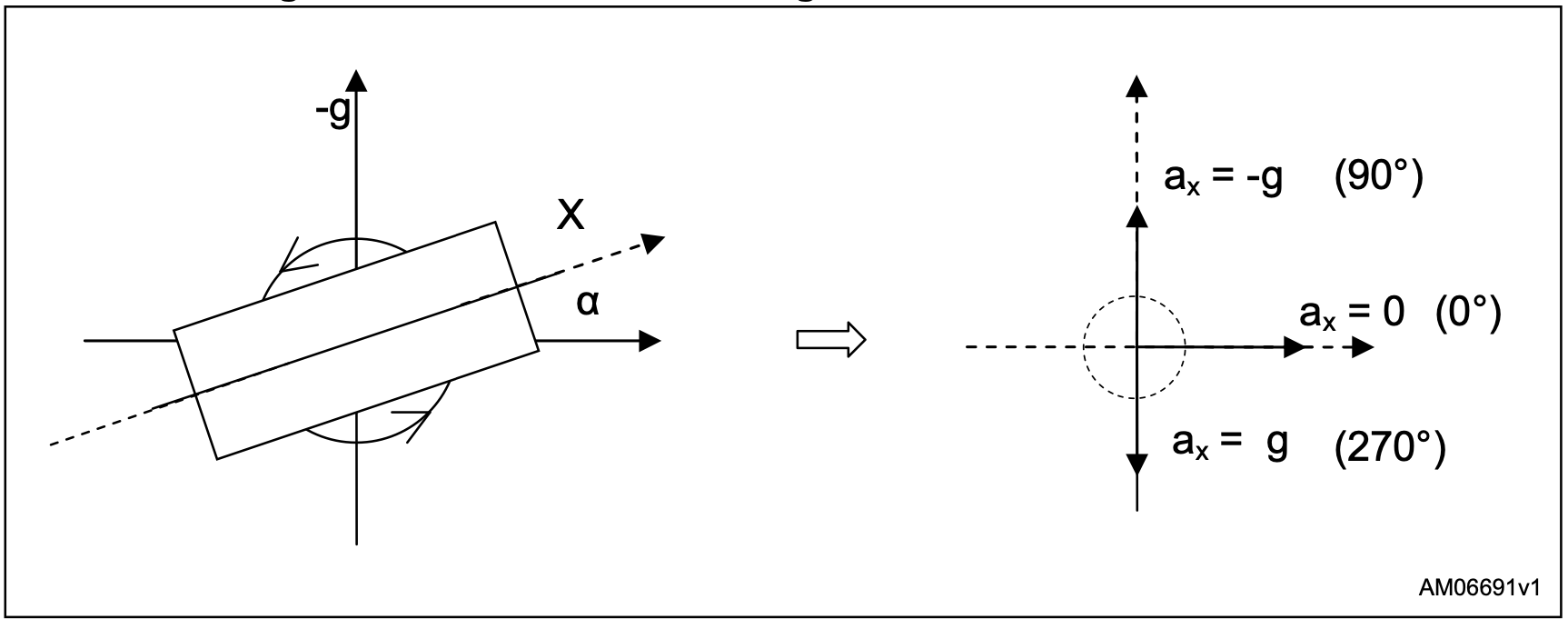
图二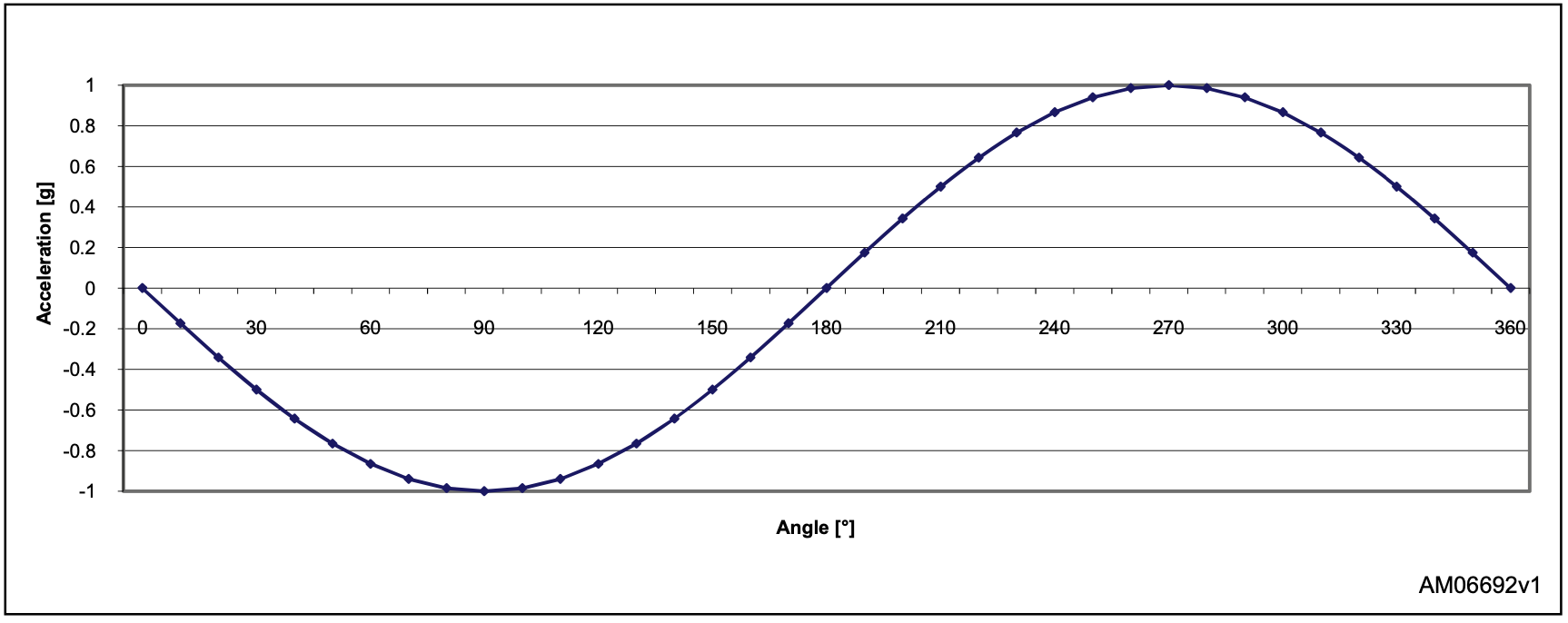
图三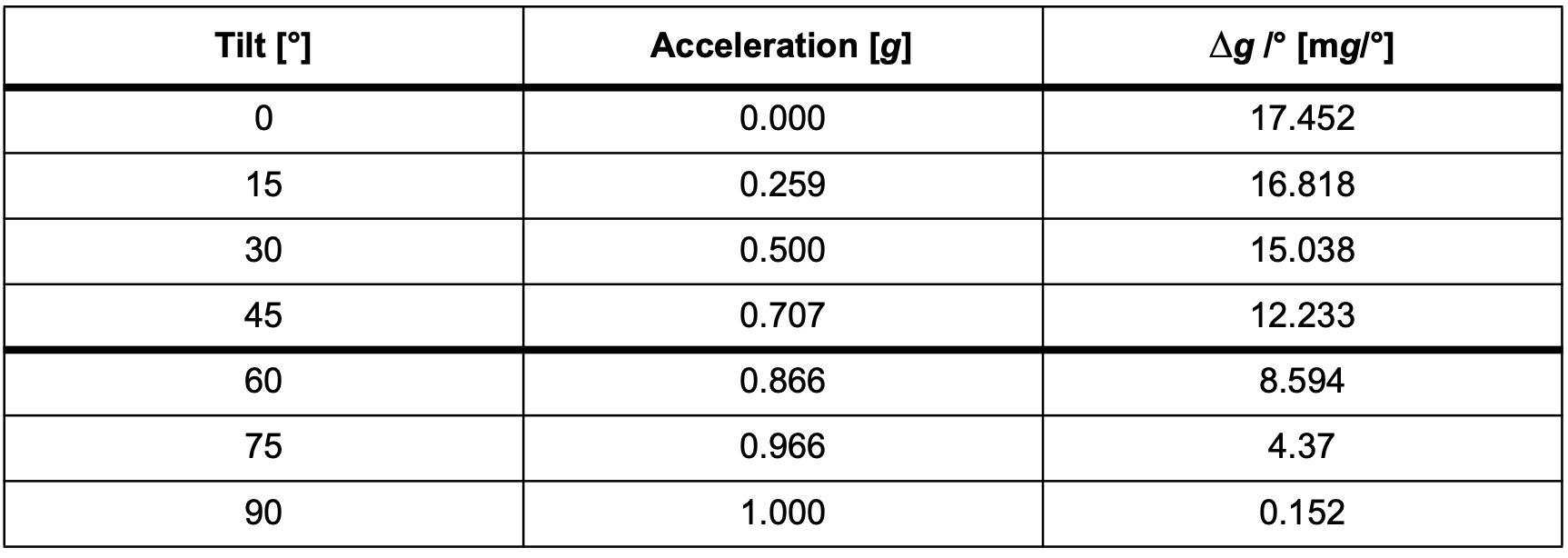
*双轴倾斜感应
当使用双轴倾斜感测方法时,应注意两种不同的情况,其中一种方法可能会限制总体精度甚至抑制倾斜计算。
下图,示例A:以角围绕虚线箭头逆时针旋转加速度计。 当小于45°时,X轴具有较高的灵敏度,而Y轴具有较低的灵敏度。 当大于45°时,X轴灵敏度较低,而Y轴灵敏度较高。 因此,当使用两轴方法时,始终建议根据正交轴将角度计算为±1 g。
下图,示例B:X和Y轴均具有高灵敏度。 但是如果没有第三轴(例如Z轴)的帮助,则不可能将30°的倾斜角与150°的倾斜角区分开,因为X轴在这两个倾斜角上具有相同的输出。
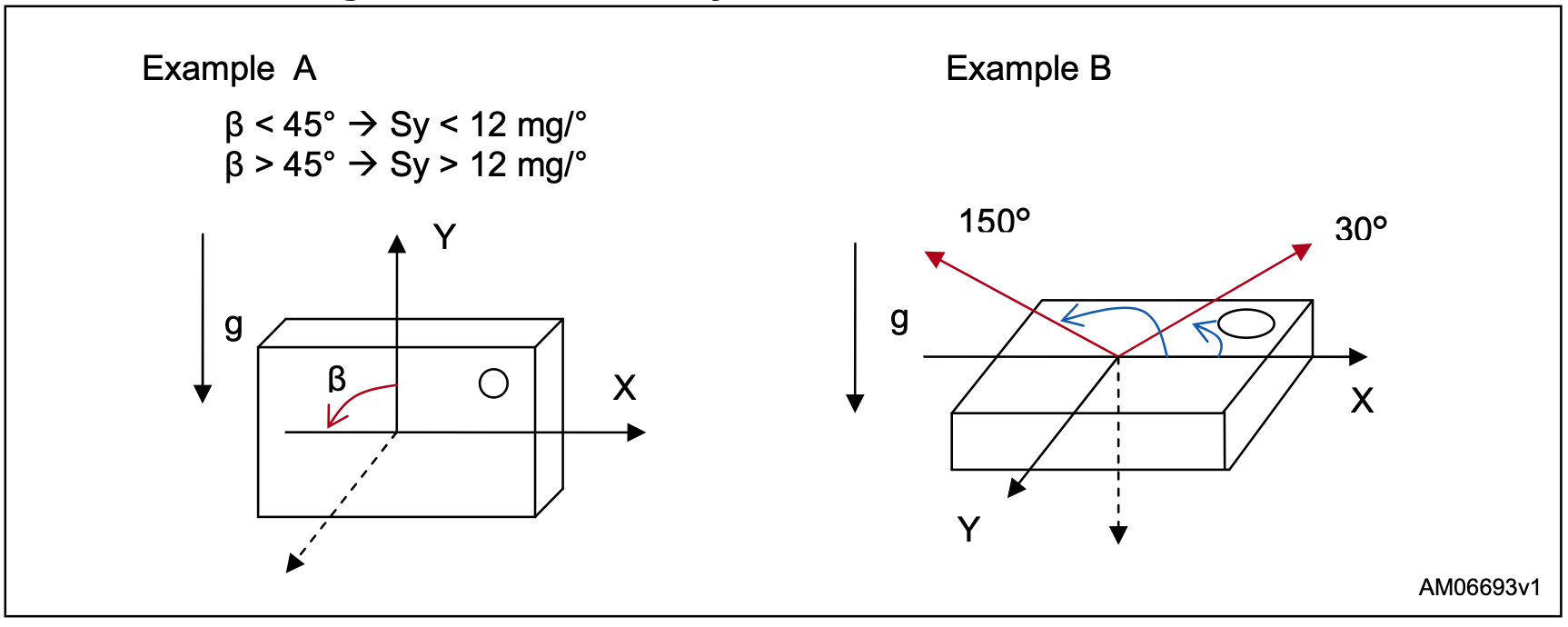
*三轴倾斜感应
使用3轴加速度计,用户可以将Z轴与X轴和Y轴结合使用以进行倾斜感测,从而提高倾斜灵敏度和精度(下图)。
有两种方法可以计算出下图中的3个倾斜角。第一种方法是使用基本三角方程式3、4和5,其中Ax1,Ay1和Az1是在对原始测量数据(Ax,Ay, Az):

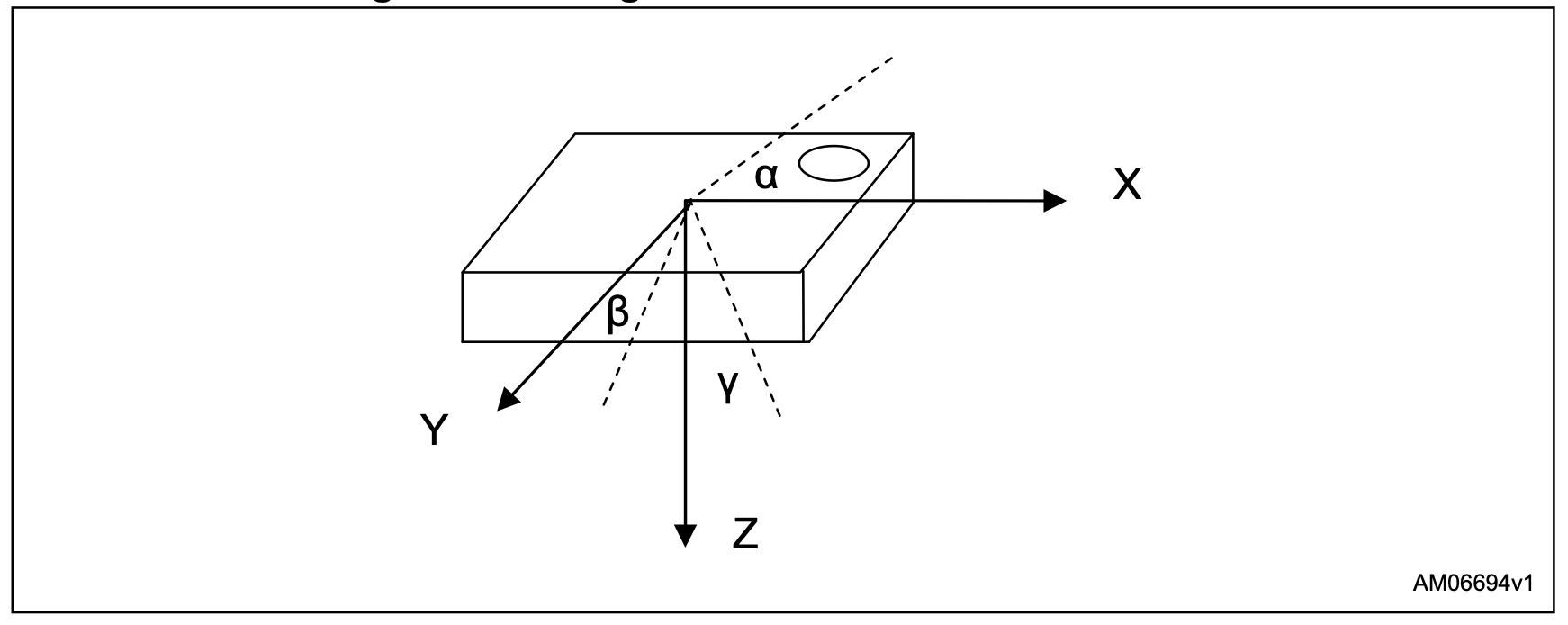
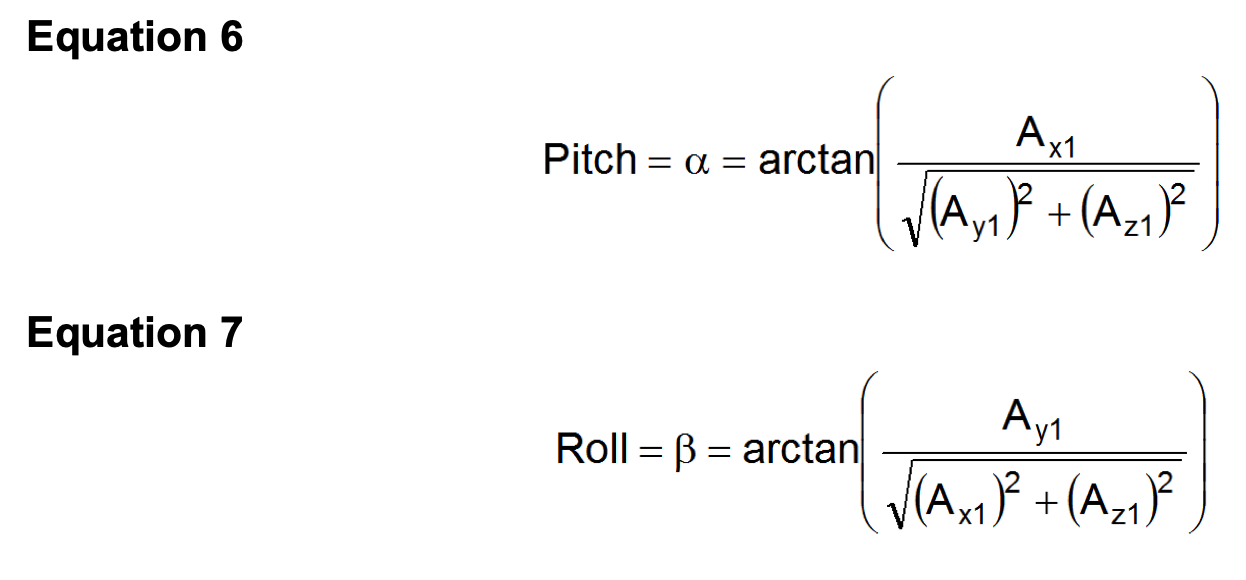
第二种方法是使用三角方程式6和7计算俯仰角和侧倾角,从而在360°旋转时产生恆定的灵敏度,如下图所示。